passpopla.blogg.se - Binomial histogram maker

BINOMIAL HISTOGRAM MAKER TRIAL

# prob: probability of success on each trialīinom_sum <- function(size, prob, lb, ub, col = 4, lwd = 1.

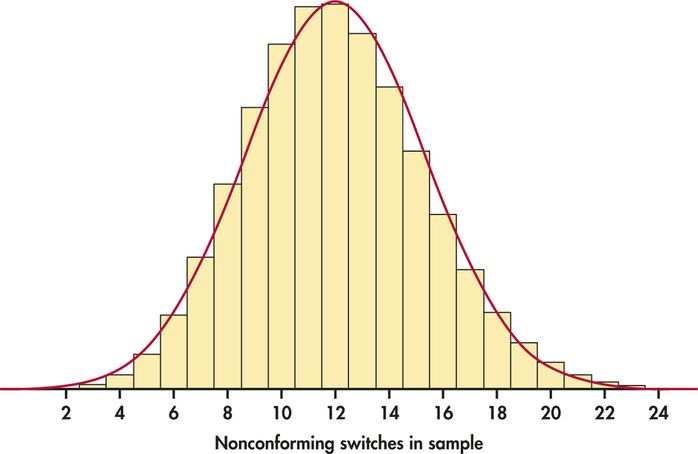
The following R function allows visualizing the probabilities that are added based on a lower bound and an upper bound. Lty = 1, col = 1:3, lwd = 2, box.lty = 0)Īs the binomial distribution is discrete, the cumulative probability can be calculated adding the corresponding probabilities of the probability function. Ylab = "P(X = x)", xlab = "Number of successes") The binomial probability mass function can be plotted in R making use of the plot function, passing the output of the dbinom function of a set of values to the first argument of the function and setting type = "h" as follows: # Grid of X-axis values

BINOMIAL HISTOGRAM MAKER TRIAL

Prob, # The probability of success on each trial In order to calculate the binomial probability function for a set of values x, a number of trials n and a probability of success p you can make use of the dbinom function, which has the following syntax: dbinom(x, # X-axis values (x = 0, 1, 2. In the following sections we will review each of these functions in detail. The following table describes briefly these R functions. 8: Random Variables and the Binomial Distribution Defining aRandom Variable. In addition, the rbinom function allows drawing n random samples from a binomial distribution in R. expenses Making a lotto profit Tippingthe scales ona bar graph Pondering. The functions of the previous lists can be computed in R for a set of values with the dbinom (probability), pbinom (distribution) and qbinom (quantile) functions.

The expected mean and variance of X are E(X) = np and Var(X) = npq, respectively.

The probability mass function (PMF) is P(X = x) = \binom(p).

Let X \sim B(n, p), this is, a random variable that follows a binomial distribution, being n the number of Bernoulli trials, p the probability of success and q = 1 - p the probability of failure:

4.1 Plot of the binomial quantile function in Rĭenote a Bernoulli process as the repetition of a random experiment (a Bernoulli trial) where each independent observation is classified as success if the event occurs or failure otherwise and the proportion of successes in the population is constant and it doesn’t depend on its size.3.2 Plot of the binomial cumulative distribution in R.2.1 Plot of the binomial probability function in R.